Deep Learning Introduction Part 2: Entropy and the Cost Function

Posted on June 23rd 2020.

This blog is part of an introductory series on deep learning. For part 1 check this page.

In this second part I will attempt to give a short introduction on entropy, and an explanation on what a cost function is.

Entropy

Entropy is a measure with which the amount of information can be quantified. It is a cornerstone of information theory and very fundamentall to much of science. The basic intuition behind entropy is that events that are likely to occur do not contain alot of information, whereas events that are unlikely to occur contain alot of information. In this way, entropy can be also seen as a measure of uncertainty: the higher the uncertainty, the higher the entropy.

Entropy is commonly measured in bits. A bit can either be a 0 or 1. With more bits you can encode more information. A way to think about bits as containers of information, is to ask:

"How many yes/no questions do I need to answer to know the exact state of an event?"

In order to explain this using an example, suppose you had a switch with 2 settings: on or off. At any time the switch can only be in one of these two settings. How many questions do you need to know the current setting of the switch? The answer is: one. Why? You only need to ask one yes/no question:

"Is the switch on?"

Now suppose we set the switch at a random setting, how much uncertainty is there of its position? 50% uncertainty, because the setting can either be 'on', or 'off'.

The formula for entropy, when measured in bits, is given as:

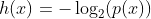
Now using this formula and filling in a probability of 50% yields:

import math

print(-math.log2(0.5))
# Output: 1

As expected, we only needed 1 question, so the information content of something that has a 50% chance happening is 1 bit. Now suppose we had 3 of these switches. How many yes/no questions would you need now to know the exact setting of all the switches? Now you need 3 questions:

"Is the first switch on? Is the second switch on? Is the third switch on?"

Now the interesting thing is that if we only had one switch, we had 2 possible settings: on or off. However, now that we have 3 switches, our switches in total have 8 different possible settings:

off off off
off off on
off on off
off on on
on off off
on off on
on on off
on on on

So now, given that we have 8 possible states, setting all switches at a random would give every setting a 1/8 chance of being the correct one. Calculating the number of bits using the above formula

import math

print(-math.log2(1/8))
# Output: 3

Now the information content is 3 bits. So as you can see the entropy of an event increases when the probability of the event decreases.

The Cost Function

Moving on to the cost function, the cost function represents the error between the predicted values of our neural network and the actual true values of our labeled data. This term is sometimes also called the loss function.

When training a neural network, we seek to minimize the cost function. What this means is that the lower the cost function is, the better our neural network is able to near the true labeled values of our dataset. To calculate the cost function we need predictions of our neural network, and labeled values.

Often the cost function is implemented as the cross-entropy between the predicted values of our neural network and the actual values of our labeled data. For us, because we have 2 classes, we will be using binary cross-entropy. The formula for binary cross-entropy is:

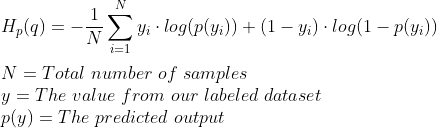
Binary Cross-entropy is a calculation of the average difference between two probability distributions. The distributions here being the true distribution we have from our labeled dataset, and the distribution predicted by our neural network.

We can use the output of our neural network to tell how confident it is of its prediction. When binary-cross entropy is used, predictions that are confident and right do not add alot to the outcome of the cost function, but predictions that are confident and wrong add alot to the value of the cost function. This can be visualized with an example. Suppose the following are a set of output values that the neural network generated, and the corresponding true values:

1: Prediction 0.9, True value 1
2: Prediction 0.9, True value 0
3: Prediction 0.3, True value 0
4: Prediction 0.5, True value 1

Recall from part 1 of this series that we assigned the value '0' to the Hazel Shrub, and the value '1' to the Alder Blackthorn Shrub. So in the first datapoint, our neural network is very confident that the datapoint is the Alder Blackthorn Shrub, and this is also its true value. The second datapoint however, our neural network is still as confident that the true value is the Alder Blackthorn Shrub, while the true value is the Hazel Shrub.

When using the equation above to calculate the binary cross-entropy for these 4 datapoints, this yields:

1 * log(0.9) + 0 * log(0.1) = - 0.152 
0 * log(0.9) + 1 * log(0.1) = - 3.3219
0 * log(0.3) + 1 * log(0.7) = - 0.5146
1 * log(0.5) + 1 * log(0.5) = - 1

- 0.152 + - 3.3219 + - 0.5146 + - 1 = -4.989
- 4.989 / 4 = -1.2471
- 4.989 * -1 = 1.2471

So the binary cross-entropy for these 4 points is 1.2471 bits. So this means that the average difference in information content between the true distribution, and our predicted distribution for an event is 1.2471 bits. As you can see, predictions that are confident and wrong contribute way more to the final value than predictions that are confident and right.

The outcome of the binary cross-entropy always is a scalar value >= 0. When all our predictions exactly equal all true values, the outcome of the binary cross-entropy is 0. However, in practice this will almost never happen, because the final output activation of our neural network is the sigmoid, and the sigmoid saturates at its limits. This is not a bad thing however, because once our cost function reaches 0, the weights and bias values of our neural network will not be updated anymore.

So now we have a neural network, and a cost function that can tell us how wrong our predictions are. What is left, is a system that can update the weights and the bias values of our neural network using the cost function. This will be the topic of the next blog in this series.

Thanks for reading this blog! Like you, I am also learning, so if you see any errors in the text, or if anything is unclear to you, please let me know.